The Price of Anarchy in Concave Pro-Rata Games for Decentralized Markets

Table of Links

Abstract and Introduction

1 The concave pro-rata game

1.1 Symmetric pure strict equilibrium

1.2 Uniqueness of equilibrium

1.3 Equilibrium payoff

2 Batched decentralized exchanges

2.1 Arbitrage

3 Conclusion and References

A Numerics

B Additional Numerics

C Relaxing strict concavity

D Rosen condition

3 Conclusion

We introduced concave pro-rata games and established several useful properties under relatively mild conditions. In particular, we showed the existence of a unique equilibrium that is symmetric and pure. This equilibrium can be computed efficiently by solving a single variable, unimodal optimization problem. We further established that the price of anarchy is Ω(n) in the number of players, relative to the optimal ‘fair’ allocation. We illustrated how concave pro-rata games connect to a recent proposal for a batched decentralized exchange and numerically studied the behavior of agents engaged in such a game in the iterated setting for a specific form of utility function. Future work includes further study of the optimal arbitrage problem for batched decentralized exchanges.

References

[1] Angeris, G., Agrawal, A., Evans, A., Chitra, T., Boyd, S.: Constant Function Market Makers: Multi-asset Trades via Convex Optimization. In: Handbook on Blockchain, p. 31. Springer, first edn. (2022)

[2] Angeris, G., Evans, A., Chitra, T.: A Note on Privacy in Constant Function Market Makers (Mar 2021)

[3] Boyd, S.P., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge, UK; New York (2004)

[4] Budish, E., Cramton, P., Shim, J.: The High-Frequency Trading Arms Race: Frequent Batch Auctions as a Market Design Response. The Quarterly Journal of Economics 130(4), 1547–1621 (Nov 2015). https://doi.org/10.1093/qje/qjv027

[5] Chitra, T., Angeris, G., Evans, A.: Differential Privacy in Constant Function Market Makers. Financial Cryptography and Data Security 2022 (2022)

[6] Daian, P., Goldfeder, S., Kell, T., Li, Y., Zhao, X., Bentov, I., Breidenbach, L., Juels, A.: Flash boys 2.0: Frontrunning in decentralized exchanges, miner extractable value, and consensus instability. In: 2020 IEEE Symposium on Security and Privacy (SP). pp. 910–927 (2020). https://doi.org/10.1109/SP40000.2020.00040

[7] Diamond, S., Boyd, S.: CVXPY: A Python-embedded modeling language for convex optimization. Journal of Machine Learning Research 17(83), 1–5 (2016)

[8] O’Donoghue, B., Chu, E., Parikh, N., Boyd, S.: Conic optimization via operator splitting and homogeneous self-dual embedding. Journal of Optimization Theory and Applications 169(3), 1042–1068 (June 2016), http://stanford.edu/~boyd/papers/scs. html

[9] Penumbra Labs: ZSwap - The Penumbra Protocol. https://protocol.penumbra.zone/main/zswap.html

[10] Rosen, J.B.: Existence and Uniqueness of Equilibrium Points for Concave N-Person Games. Econometrica 33(3), 520 (Jul 1965). https://doi.org/10.2307/1911749

[11] Selten, R.: Preispolitik der Mehrproduktenunternehmung in der statischen Theorie (1970)

[12] Von Neumann, J., Morgenstern, O.: Theory of games and economic behavior. In: Theory of games and economic behavior. Princeton university press (2007)

[13] Walther, T.: Multi-token Batch Auctions with Uniform Clearing Prices (Jul 2018)

A Numerics

The results of §1 provide insight into the equilibrium behavior of concave pro-rata games. Here we explore the transient behavior of such games through simulation.

Shared equilibrium. The (unique) symmetric pure equilibrium strategy is the solution to problem (4). This is easy to compute using the first order optimality conditions for problem (4) given in (6). Plugging in this particular form of f, we obtain the following quadratic equation:

For more details, the code is available at (anonymized for review).

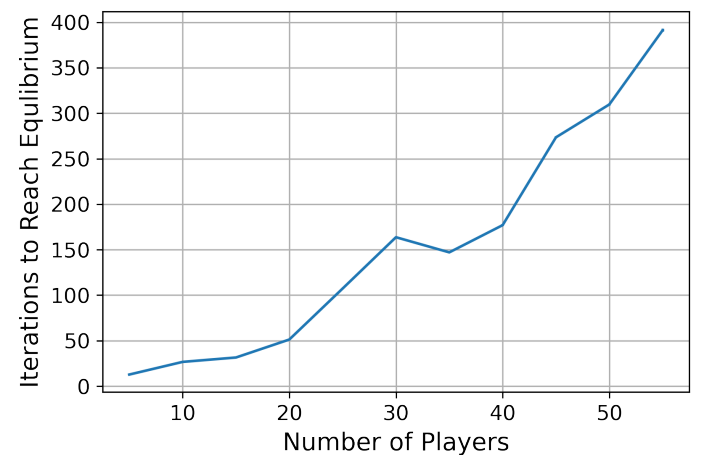
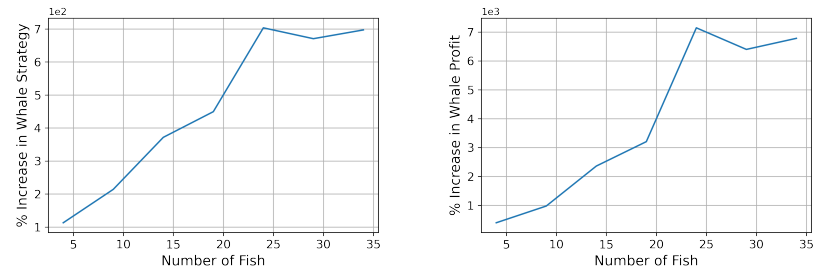
B Additional Numerics

Here we expand on the simulations introduced in appendix A using a class of utility function that allows us to express many quantities of interest in closed form.

Game setup. We consider the following three scenarios:

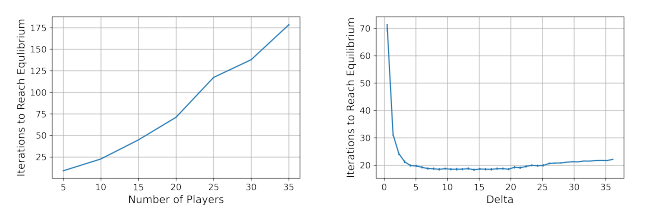
Simulation results. In our simulations, we fix β = 0.5 and γ = 0.05. We average each reported value over 100 trials. In figure 4, the intial strategy of each player is drawn uniformly at random from the interval (0, w/n), where w is a value such that f(w) = 0.

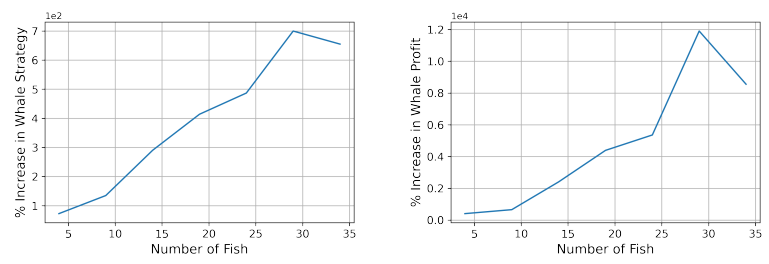
The left plot of figure 4 illustrates that the number of iterations needed to reach the unique equilibrium, in the absence of budget constraints, scales superlinearly in the number of players. The right plot demonstrates that in the scenario of bounded strategy updates, for small values of δ, the number of iterations required to reach equilibrium increases significantly when compared to the unbounded strategy update scenario.

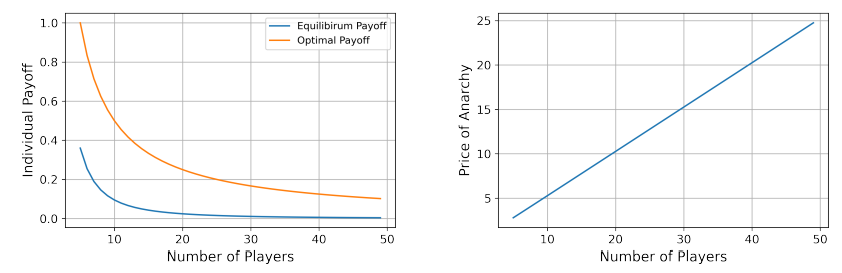
Price of Anarchy The equilibrium payoff can easibly be found to be

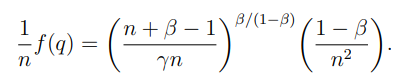
Similarly, it can be show that the optimal payoff conditioned on every agent receving the same payoff is given by

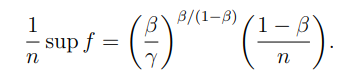
We obtain the price of anarchy by taking the ratio of the equilibrium payoff and the optimal payoff:

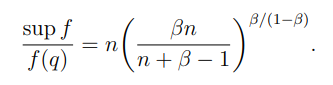
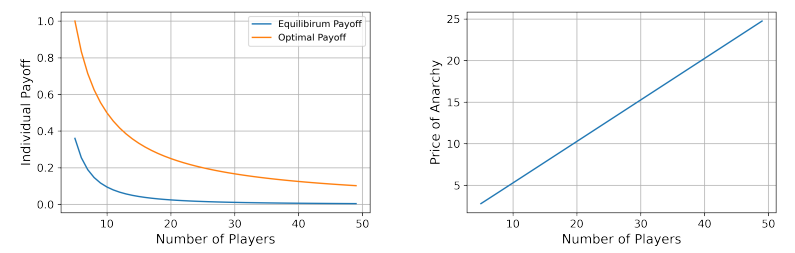
We again fix β = 0.5 and γ = 0.05. The left plot of figure 6 illustrates the optimal payoff function and the equilibrium payoff function as a function of the number of players n, while the right plot of figure 6 illustrates the price of anarchy as a function of n.

C Relaxing strict concavity

The statement above follows from the negation of both (a) and (b). This equivalence has a simple interpretation: if the point (0, 0) is collinear with any other two points on the graph of f, {(s, f(s)) | s > 0}, then the function f is a piecewise function with a linear segment starting at 0. The converse of this is that if the function f has no linear segment around 0 (i.e., every linear over estimator around 0 lies strictly above f) then any chord must lie strictly below the function.

D Rosen condition